Le problème de Tam ...

Les objectifs

  • Travailler la capacité de "voir dans l'espace"

  • "Visualisation" une section

  • illustrer la nature des sections planes pour créer des images mentales

  • Conjecturer les effets d'une réduction ou d'un agrandissement sur les volumes

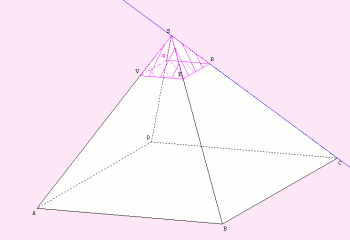
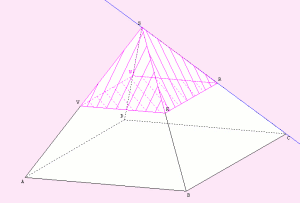
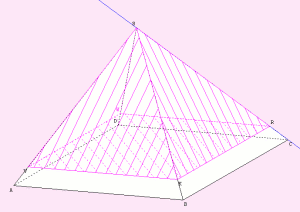
Exercice 1 Première partie : représentation du problème
1. Représente une pyramide régulière à base carrée et place un point R sur (SC).
2. Représente la section de cette pyramide avec le plan p1 passant par R et parallèle à la base. Quelle est la nature de cette section ?
3. Note K, V et W les points d'intersection de p1 avec les droites (SB), (SA) et (SD).
4. Hachure les faces du solide SRKVW.
5. Observe les différentes pyramides obtenues en faisant varier la position du point R sur la droite (SC).

Aide logiciel : charger un solide

Charger une pyramide régulière à base carrée : Fichier - Charger une figure - Figures de base.

Pour connaître le nom de ce solide

    

Aide logiciel : créer une droite

Créer - Ligne(s) - Droite - définie par 2 points

    

Aide logiciel : créer un point libre

Créer - Point - Point libre - Point sur une droite

    

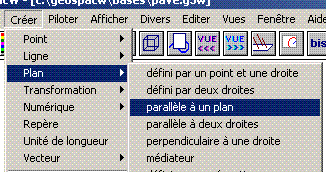
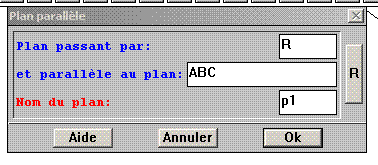
Aide logiciel : créer un plan parallèle à une face passant par un point

Créer - Plan - Plan parallèle à une face.

  


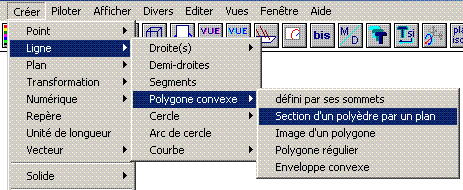
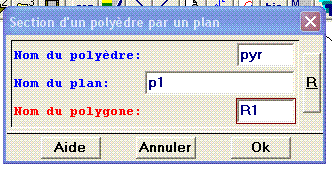
Aide logiciel : visualiser une section

Créer - Ligne - Polygone convexe - Section d'un polyèdre par un plan

  

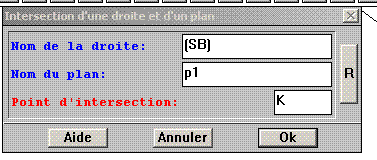
Aide logiciel : créer un point à l'intersection d'une droite et d'un plan

Créer - Ligne(s) - Droite - définie par 2 points

    

Aide logiciel : Hachurer les faces d'un solide

Il faut d'abord définir le solide dont tu veux hachurer les faces.




Remplis la fiche élève et appelle le professeur.


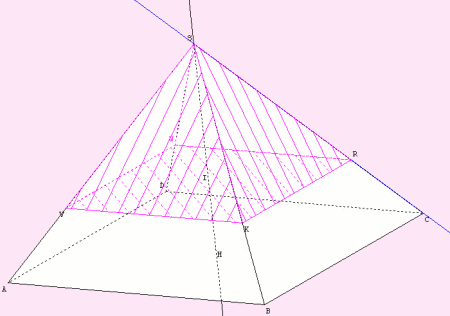
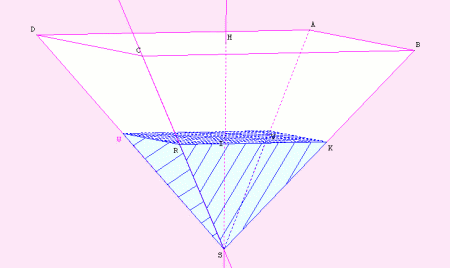
Exercice 2 : On appelle [SH] la hauteur de la pyramide SABCD et [SI] celle de SRKVW.
1. Construis la droite (d) passant par S et perpendiculaire à la base de la pyramide SABCD.
2. Construis H comme point d'intersection de (SH) et de la base.
3. Explique sur ta fiche une autre méthode de construction possible pour H.
On admettra que (SH) est aussi perpendiculaire à la base de SRKVW .
4. Complète : le point I est le point d'intersection de la droite ............et du plan........
5. Construis I.

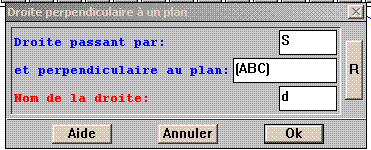
Aide logiciel : créer une droite perpendiculaire à un plan

Créer - Ligne - Droite - Perpendiculaire à un plan

  

Aide logiciel : créer un point à l'intersection d'une droite et d'un plan

Créer - Point - Intersection droite-plan

  

Remplis la fiche élève et appelle le professeur.


Exercice 3 : la pyramide de Tam
On admet que SRKVW est une pyramide régulière.
Pour mieux visualiser le problème, tu peux retourner ta pyramide !
1. Affiche les longueurs SI et SH.
2. Crée la pyramide régulière SRKVW. Tu l'appelleras pyr2.
3. Affiche les volumes respectifs v1 et v2 des pyramides SABCD et SRKVW.
4. Trouve la valeur correspondant au cas de Tam. Que penses-tu de sa conjecture ?
5. Que peux-tu conjecturer ? :le volume de la grande pyramide semble ..... fois plus grand que le volume de la petite pyramide.

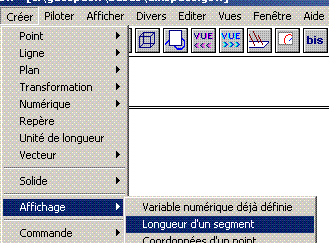
Aide logiciel : longueur d'un segment

Créer - Affichage - Longueur d'un segment

  


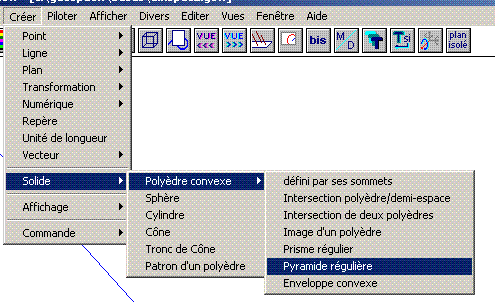
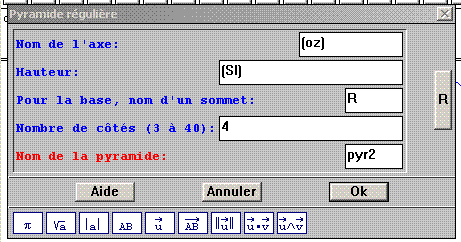
Aide logiciel : créer une pyramide régulière

Créer - Solide - Pyramide

  


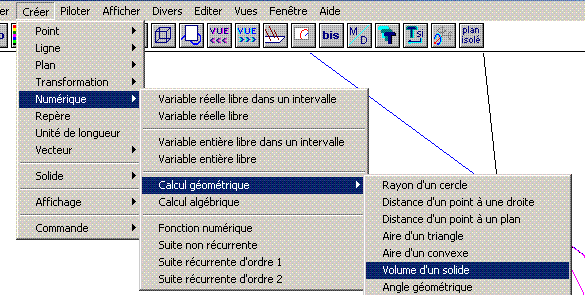
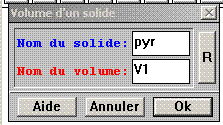
Aide logiciel : calculer un volume

Créer - Numérique - Calcul géométrique - Volume d'un solide


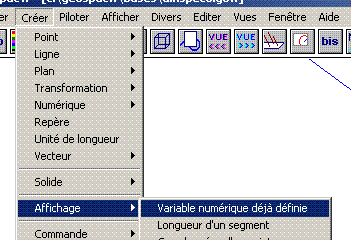
Aide logiciel : afficher un volume calculé

Créer - Solide - Pyramide


Exercice 4 :Nous allons démontrer cette conjecture. Dans cet exercice, I est le milieu de [SH]. Les dimensions des pyramides sont inconnues.
1. Exprime v1 en fonction de AB et SH.
2. Complète : SH = ...... x SI
3. Déduis-en que v1= (2/3) x AB2 x SI

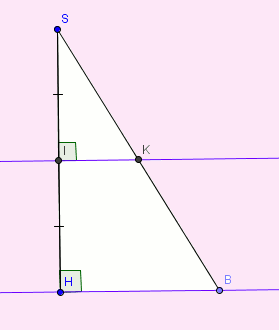4. Dans le triangle SHB, prouve que SB = 2 x SK


(on admet que (IK) et (HB) sont perpendiculaires à (SH)).


5. Dans le triangle SAB, prouve que AB = 2 x VK


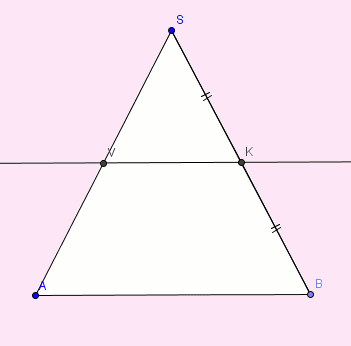(on admet que (VK) et (AB) sont parallèles).

6. Déduis-en que v1=8xv2

haut