Les documents suivants sont rangés dans l'ordre de la progression 2026/2027 :
|
Outils pour réussir








|
Expressions numériques (1) : priorités opératoires
Connaître et utiliser les priorités opératoires.




|






|
Symétrie centrale ou demi-tour (1)
Construction de figures à l'aide d'un papier calque. Définition et construction du symétrique d'un point à la règle et au compas. Retour sur la symétrie axiale.


|


|
Nombres relatifs (1) : introduction et repérage sur une droite graduée
Nombres relatifs : définition et repérage sur une droite graduée. Comparaison.



|



|
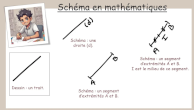
Introduction à la démonstration


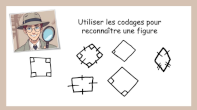
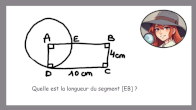

|
Problèmes algébriques









|
Proportionnalité (1)
Identifier des situations de proportionnalité dans des contextes concrets (prix, recettes,distances, échelles). Utiliser un coefficient
de proportionnalité dans des contextes concrets(prix unitaire, vitesse moyenne, échelle, etc.).








|
 





|
Multiples et diviseurs
Division euclidienne, diviseurs et multiples. Critères de divisibilité. Résoudre des problèmes impliquant quotient et reste. L’algorithme de la division est l’occasion de faire vivre ces
notions (trouver les diviseurs d’un nombre, compter le nombre de diviseurs…) avec Scratch ou tableur.



|




|
Calcul littéral (1) : Produire des formules


|

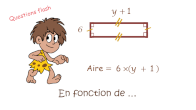


|
Nombres relatifs (2) : repérage dans le plan



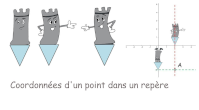
|



|
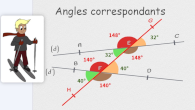
Angles (1) caractérisation du parallélisme


|


|
Calcul littéral (2) : substitutions
Produire une expression littérale. Substituer une valeur numérique à une lettre pour calculer la valeur d’une expression.



|



|
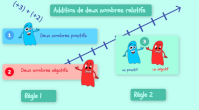
Nombres relatifs (3) : addition de relatifs


|


|
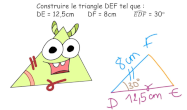
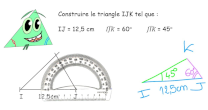
Angles (2) somme des angles d'un triangle
En 6ème, les élèves ont utilisé cette propriété sans la démontrer.En 5ème, ils la démontrent en utilisant les angles alternes-internes ou
la symétrie centrale.Savoir l’appliquer aux cas particuliers du triangle équilatéral, d’un triangle rectangle, d’un triangle isocèle.
L’utiliser pour construire des triangles en vraie grandeur à partir de données partielles.









|

|



|
Aires et périmètres (1)


|
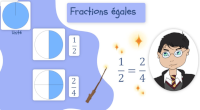
Fractions (1) : comparaison
L’élève compare des fractions par la méthode la plus adaptée
(fractions égales, comparaison à 1, comparaison à 0,5). L’élève
compare des proportions.




|



|
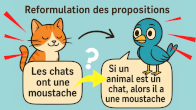
Démontrer (2) Propriété réciproque et propriété caractéristique





|
Symétrie centrale ou demi-tour (2)
Comprendre l’effet des symétries (axiale et centrale) sur des figures : conservation du parallélisme, des longueurs et des angles. Identifier des symétries dans des frises, des pavages, des rosaces.



|
Diviser par un nombre décimal
Ramener une division dont le diviseur est décimal à
une division dont le diviseur est entier grâce aux égalités de fractions.
|
Parallélogrammes (1)
Constructions. Propriétés caractéristiques.




 Défi calculatrice :
Défi calculatrice : 
|
Probabilités
Expérimenter des jeux de hasard : pièces, dés, urnes, roues de loterie. Verbaliser des exemples d’issues ou d’événements.
Choisir de décrire une situation par une équiprobabilité des issues, en justifiant ce choix par un
argument de symétrie ou en l’absence d’argument en faveur d’une non équiprobabilité : dé
équilibré ou tirage d’objets identiques dans une urne. Comprendre que ce choix peut être mis en question dans
certaines circonstances (dé pipé, objets de tailles ou de
masses différentes dans une urne).Répéter matériellement une expérience aléatoire simple. Enregistrer les
résultats observés dans un tableau d’effectifs et de fréquences.





|
Expressions numériques (3) : structure d'une expression numérique
Traduire une expression numérique par une phrase et écrire une expression numérique décrite par une phrase.






|
Aire du disque





|


|
Nombres relatifs (4) : soustraction de relatifs
Soustraction de nombres relatifs.




|
Parallélogrammes particuliers
Le rectangle est défini comme un parallélogramme ayant un
angle droit ; le losange comme un parallélogramme ayant deux
côté consécutifs égaux ; le carré comme étant à la fois un
rectangle et un losange.
Justifier les propriétés caractéristiques du rectangle, du
losange, du carré.
Construire ces quadrilatères en utilisant la définition ou
une propriété caractéristique.
Utiliser une propriété caractéristique sur les
diagonales ou les côtés pour les construire ou donner la nature
du quadrilatère.
Savoir que les carrés sont des losanges et des
rectangles.
Par exemple, dans la configuration suivante : le triangle DRO
est rectangle en R. On construit les points L et E images
respectives des points D et O, par le demi-tour de centre R.
L’élève sait justifier la nature du quadrilatère DOLE.
|
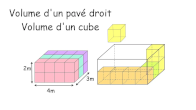
Patrons et volume du pavé droit et du cube
Patron d'un pavé droit et d'un cube. Assemblage de solides simples.




|
Carrés et cubes
Connaître les carrés des entiers de 1 à 12. Savoir écrire un nombre sous la forme d'une puissance de 2 ou de 3.
Enchaîner des calculs contenant des puissances simples. |


|
|
Tracer le cercle circonscrit dans les triangles particuliers. Observer puis admettre qu’un triangle rectangle est inscrit dans un demi-cercle dont le diamètre
est l’hypoténuse.



|
Structure d'une expression littérale
Selon la dernière opération à effectuer en suivant les règles
de priorité, l’élève sait dire si une expression littérale est une
somme ou un produit, afin de préparer la distributivité.
|
Triangles : calculs d'aire



|
Expressions numériques (4): distributivité simple
Utiliser la formule de distributivité avec des nombres. Développements et factorisations.




|
Fractions (2) : additions et soustractions
Addition et soustraction des fractions dont les dénominateurs sont quelconque.
|
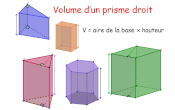
Prismes droits et cylindres de révolution (1)




 Narration de recherche :
Narration de recherche :

|
Expressions numériques (5) : pour résoudre un problème
Traduire un problème à l'aide d'une expression numérique.



|
Carrés et cubes (2) : calcul littéral
Calculer la valeur d'une expression littérale contenant une puissance simple.
|
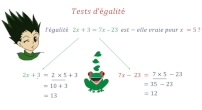
Calcul littéral (2) : tests d'égalité
Tests d'égalité avec et sans calculatrice.



|
Aire du parallélogramme et de figures complexes
Déterminer l'aire du parallélogramme et l’aire de figures complexes construites à partir de
parallélogrammes et du disque.






|
Nombres relatifs (5) : sommes algébriques





 TICE et problèmes 5 :
TICE et problèmes 5 : 
|
Statistiques (1)
Le travail commencé en sixième de définition d’une enquête, de son sujet,
de la population à étudier, du questionnaire à élaborer, de la collecte des
données, etc. est poursuivi.
Par exemple, le professeur peut organiser, en groupe, un sondage sur les
élèves de la classe ou de plusieurs classes (temps passé sur les écrans,
nombre d’heures de sommeil, nombre de frères et sœurs, …), recueillir les
réponses à ce sondage, et demander aux élèves à les organiser sousforme
de tableau ou de graphique, puis utiliser les indicateurs statistiques
(moyenne, fréquences) pour commenter les résultats.Comprendre comment évolue une moyenne lorsque toutes les
données varient de façon identique.








|
Fractions (3) : résolution de problème avec des fractions
Utilisation des modèles en barre.
|
Calcul littéral (3) : réductions
Utiliser la distributivité simple pour réduire une expression littérale de la forme ax + bx où a et b sont des nombres décimaux.


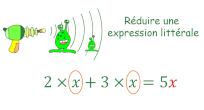




|
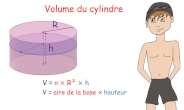
Prismes et cylindres (2)


 
|
Pourcentages






|
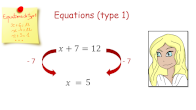
Equations x + a = b
Vocabulaire (inconnue, équation). Méthode de résolution.


|
Triangles (3) : Hauteurs et orthocentre


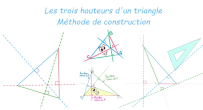

|
Démontrer (3) Utiliser le calcul littéral pour prouver une propriété
L’élève mobilise le calcul littéral pour généraliser un résultat (conjecture numérique, etc.).
La notion de contre-exemple est introduite. Par exemple, il montre que la somme de deux nombres pairs
est paire (preuve utilisant le calcul littéral). La somme de deux carrés parfaits n’est pas (nécessairement) un carré parfait
(contre-exemple).Formuler des conjectures en s'appuyant sur un algorithme ou un tableur.



|
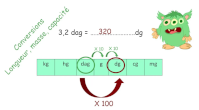
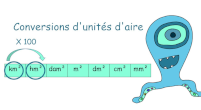
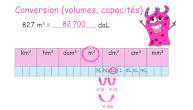
Conversions
Résoudre des problèmes
faisant appel à des
conversions d’unités de
longueur et d’unités
d’aires. Effectuer des conversions d’unité de volume et de
capacité. Il sait que 1 L est égal à 1 décimètre cube.









|
Proportionnalité (5) : Echelles



|
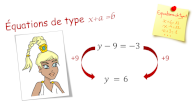
Equations de type 2





|
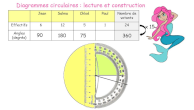
Statistiques (2)
Prélever des données numériques à partir de supports variés. Produire des tableaux, diagrammes et graphiques organisant des données
numériques. Exploiter et communiquer des résultats de mesures. Tableaux, diagrammes en bâtons, circulaires ou semi-circulaires, graphiques
cartésiens. Choisir une représentation adaptée à ce qu’il convient de mettre en avant.




|
Représentation graphique d'une situation de proportionnalité
Représenter une situation de proportionnalité par un tableau ou un graphique. Remarquer puis
admettre que dans une situation de proportionnalité les points sont alignés avec l’origine du
repère dans la représentation des données.
|
Symétrie centrale (3)


|
|
Connaître et construire les médianes d’un triangle. Observer
qu’elles sont concourantes en un point appelé centre de gravité.
Démontrer la propriété : une médiane partage un
triangle en deux triangles d’aires égales.
|
Notion de fonction
Introduire l’expression: « en fonction de » dans des contextes concrets ou mathématiques. Produire un tableau de
valeurs.Lire et interpréter un tableau de valeurs. Placer dans un repère orthogonal donné des points correspondant
à un tableau de valeurs. Lire un graphique cartésien donné par une courbe ou un nuage de points.





|



























































