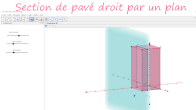
Section de solide par un plan (1) : premières observations

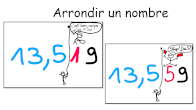
AP Théorème de Pythagore

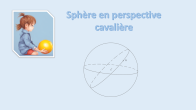
Sphère et boule

Définitions, section par un plan. Aire de la sphère, volume de la boule.

Notion de fonction

Déterminer l’image d’un nombre par une fonction déterminée par une courbe, un tableau de données ou une formule. Déterminer un antécédent par lecture directe dans un tableau ou sur une représentation graphique.

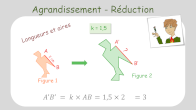
Agrandissement/Réduction (1)

Effet sur les longueurs et les aires.

Résoudre des problèmes faisant appel aux fractions

Les fractions sont utilisées pour résoudre des problèmes du type : « Le premier mai, un marchand de muguet a vendu les trois quarts de ses bouquets le matin et les deux cinquièmes du reste l’après-midi. Sachant qu’il lui reste 12 bouquets, combien de bouquets avait-il au début de la vente ? ». Les schémas en barres vus les années précédentes sont utilisés autant que de besoin.

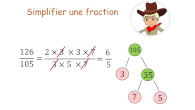
Simplifier des fractions

Rendre irréductible une fraction par simplifications successives.

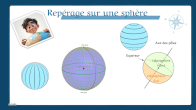
Repérage sur la sphère - Coordonnées géographiques (latitude, longitude)

Translations et vecteurs

AP Nombres rationnels

Additions, soustractions, multiplications et divisions de nombres rationnels : rappels des années antérieures.

Vecteurs égaux, opposé d'un vecteur, vecteur nul

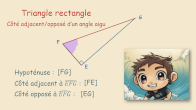
AP Cosinus d’un angle aigu

Rappel : utilisation du cosinus pour calculer une longueur dans un triangle rectangle.

AP Réductions d'expressions littérales

Simplifications d'écritures de sommes et de produits.

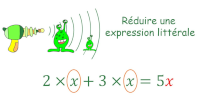
Parenthèses précédées d'un signe + ou -

Suppression de parenthèses et réductions de sommes algébriques.

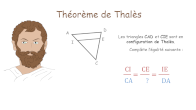
Théorème de Thalès : cas des triangles emboîtés et configuration papillon

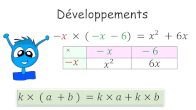
AP : distributivité simple

Rappels de cours et entraînement.

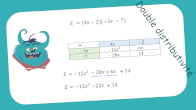
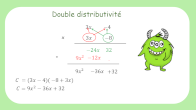
Double distributivité

Développements.

Fonctions linéaires

Définition d'une fonction linéaire. Calculs d'images et d'antécédents. Déterminer une fonction linéaire connaissant un nombre et son image.

Statistiques (1) : effectifs cumulés croissants

À partir d’un tableau d’effectifs, l’élève calcule les effectifs cumulés croissants.

AP : puissances de 10

Rappels de cours et entraînement.

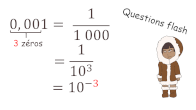
Contraposée et réciproque du théorème de Thalès

Prouver que deux droites ne sont pas parallèles. Prouver que deux droites sont parallèles.

Probabilités (1) $P(A\cup B)$

En situation d’équiprobabilité, l’élève calcule une probabilité en prenant le rapport du nombre de cas favorables au nombre total de cas. L’élève calcule des probabilités d’événements faisant intervenir « ou », « et » « ou exclusif ». Pour des expériences aléatoires à deux épreuves indépendantes, l’élève représente ou utilise des arbres de dénombrement ou des tableaux.

Identités remarquables (1) : développer

Manipuler les trois identités remarquables pour développer.

Agrandissement/réduction 2 : effet sur les volumes

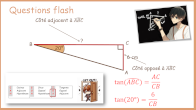
Trigonométrie : calcul d'une longueur dans un triangle rectangle

Puissances d'exposants positifs et négatifs - Ecriture scientifique

En prenant appui sur la puissance de 10 d’exposant négatif, l’élève est conduit à la généraliser pour une base quelconque.

Somme de 2 vecteurs, relation de Chasles

Identités remarquables (2) : factoriser

Manipuler les trois identités remarquables pour factoriser.

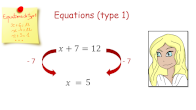
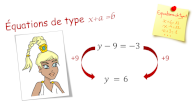
AP: retour sur les équations

Parcours équations en 4 Genially :

Multiplier et diviser des puissances

Les formules sur les puissances de 10 sont généralisées à une base quelconque.

Trigonométrie : calcul d'un angle aigu dans un triangle rectangle

Fonctions affines et représentation graphique

Définition d'une fonction affine ; image d'un nombre ; courbe représentative dans un repère. Vocabulaire : coefficient directeur, ordonnée à l'origine.

Mise en équation et résolution de problèmes à l'aide d'une équation du premier degré du type ax+b=cx+d

Quartiles et médianes

En utilisant les effectifs cumulés croissants, l’élève détermine la médiane et les premier et troisième quartiles (Q1 et Q3) d’une série statistique.

Représentation graphique et configuration de Thalès

L’élève fait le lien entre le théorème de Thalès et la proportionnalité. À l’aide du théorème de Thalès, l’élève démontre que l’alignement des points avec l’origine caractérise la proportionnalité.

Equations produits

La résolution d’équation permet de travailler sur la notion d’équivalence. Ainsi le professeur explicite ce que signifient des équations équivalentes. Lors d’une résolution, il précise si le raisonnement s’appuie sur des équations équivalentes ou sur une analyse-synthèse. L’usage du symbole <=> est limité, et toujours justifié, au moins oralement.

Fonctions affines (2)

Calculer l'antécédent d'un nombre par une fonction affine.

Simplifier des expressions multiplicatives ou des rapports

Simplifier des expressions telles que (a²b)x(bc). $\frac{a{b}^2}{a^{2}b};\frac{\pi R^2}{2\pi R}.$

Boîtes à moustache

L’élève construit des boîtes à moustache comprenant les éléments suivants : valeur minimum, premier quartile, médiane, troisième quartile, valeur maximum, en veillant de bien faire figurer l’échelle.

Caractérisation vectorielle du milieu d'un segment

Retour sur les transformations

Reconnaître une transformation.

Démontrer l'égalité (cos(a))²+(sin(a))²=1

Pourcentages : augmentation et réduction

Ecriture scientifique : résolution de problèmes

L’élève mobilise ses connaissances sur les puissances pour résoudre des problèmes issus d’autres disciplines du type « La vitesse de la lumière est 3 × 108 m/s. Le Soleil se situe à 150 millions de km. Quel est le temps mis par la lumière pour parcourir la distance du Soleil à la Terre ? ».

Fonction carré

L’élève représente la fonction carré.

Equations x²=a

Résoudre analytiquement et graphiquement des équations de la forme x²=a. Écrire l’ensemble des solutions.

Tableur et interprétation

L’élève compare deux séries statistiques en analysant les « boîtes à moustache ». Le travail commencé en 5e et 4e sur la représentation de données et sur l’utilisation des fonctions dans le tableur est poursuivi.

Probabilités (2) : simulations

Simuler des expériences aléatoires indépendantes. Observer la stabilisation des fréquences lorsqu’on augmente le nombre de répétitions de l’expérience aléatoire, faire le lien entre fréquence et probabilité en fonction du nombre de répétition. L’objectif est de faire percevoir que, quand le nombre de répétitions augmente, les fluctuations dues au hasard diminuent, et que la fréquence observée approche mieux la probabilité théorique.

Résoudre des problèmes utilisant la racine carrée

L’élève consolide sa maîtrise de la racine carrée dans le cadre de la résolution de problèmes. Par exemple : étude de l’intersection d’un cercle et d’une droite, avec discussion selon la distance de la droite au centre du cercle. Contextualiser avec la géométrie.