Documents annexes

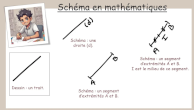
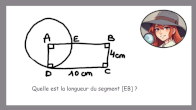
Introduction à la démonstration

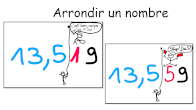
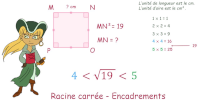
Les carrés parfaits de 1 à 144 - Racine carrée - Encadrements

Curvica

Premier travail de groupe sur la notion d'aire et de périmètre.

Arithmétique 1

Multiples et diviseurs. Résolution de problèmes.

Retour sur les sommes algébriques

Théorème de Pythagore : découverte

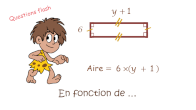
Retour sur le calcul littéral

Produire une expression littérale. Substitutions. Tests d'égalité avec et sans calculatrice.

Translations (1)

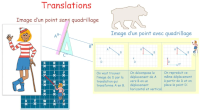
Comprendre l'effet d'une translation sur une figure. Construire l'image d'un point et d'un polygone avec et sans quadrillage.

Programmes de calcul

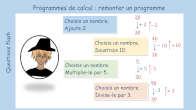
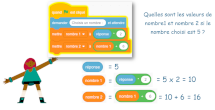
Théorème de Pythagore (1)

Théorème de Pythagore et première application : calcul de la longueur d l'hypoténuse d'un triangle rectangle.

Tester une égalité

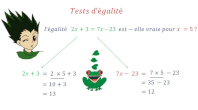
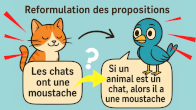
Démontrer (2) Propriété réciproque et propriété caractéristique

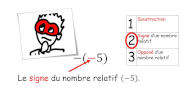
Produit de nombres relatifs

Multiplication de deux nombres relatifs.

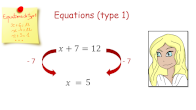
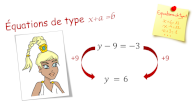
AP : retour sur les équations x + a = b

Vocabulaire (inconnue, équation). Méthode de résolution.

Quotient de deux nombres relatifs

Multiplication de deux nombres relatifs.

Puissances de 10

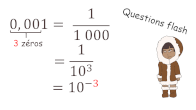
Nombres rationnels : différentes écritures - produits

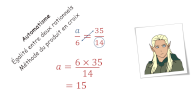
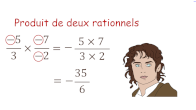
Probabilités

Utiliser le vocabulaire et les notations ensemblistes pour décrire une expérience aléatoire dans des cas simples. Définir : événement complémentaire, réunion, intersection, ensemble vide (événement impossible). Calculer la probabilité d’un événement et de son complémentaire.

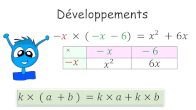
Distributivité : développements d'expressions littérales

Déterminer une quatrième proportionnelle - Proportionnalité et représentation graphique

Diverses procédures auxquelles s'ajoute celle du produit en croix.

Multiplier et diviser des puissances de 10 - Utiliser des formules

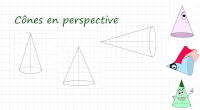
Pyramides et cônes de révolution

Perspective, représentation.

Théorème de Pythagore (2)

Calcul de la longueur d'un des côtés de l'angle droit.

Factorisation et réduction d'expressions littérales

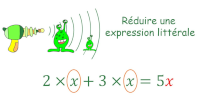
Probabilités (2) : exemples simples d’expériences aléatoires à deux épreuves

Dans le cas de deux pièces ou de deux dés, le professeur amène l’élève à bien distinguer les deux épreuves : par exemple, en faisant deux lancers successifs ou, en cas de lancer simultané, en introduisant dans un premier temps une façon d’opérer cette distinction (par exemple, lancer simultané de deux dés de couleur ou de taille différente).

Passeport Educfi

Nombres rationnels : addition et soustraction

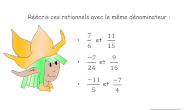
AP équations de type 2

Réciproque ou contraposée ?

Mener un travail de logique sur la réciproque et la contraposée. Travail sur le raisonnement par l'absurde.

Ce triangle est-il rectangle ?

Réciproque du théorème de Pythagore (pour prouver qu'un triangle est rectangle) et utilisation de la contraposée du théorème pour prouver qu'un triangle n'est pas rectangle.

Grandeurs quotients : utiliser les grandeurs quotients avec ou sans unité

Dans le cas où les grandeurs sont de natures différentes le coefficient de proportionnalité est une grandeur quotient dont l’unité est composée des deux unités en présence (€/L, €/kg, €/m, etc.), à laquelle il convient de donner du sens (consommation, vitesse, masse volumique, etc.).

Calculer et représenter la fraction d'une fraction

À l’aide d’un exemple à valeur générique, l’élève sait que la fraction d’une fraction se calcule par le produit des deux fractions. Calculer la fraction d'une fraction d'un nombre, d'une quantité. Produire et interpréter.

Statistiques : moyennes, médianes et étendue

Calculer une moyenne pondérée dans le cas d’une série discrète (on se limitera à de petits effectifs). Déterminer une médiane dans le cas d’une série de petit effectif présentée sous forme de données brutes. Calculer et interpréter l’étendue d’une série présentée sous forme de données brutes, d’un diagramme en barres, d’un diagramme circulaire. Comprendre l’évolution de la médiane et de la moyenne quand on ajoute une valeur extrême.

Equations de type ax + b = c. Mise en équation

Calculer avec des pourcentages.

L’élève détermine le pourcentage relatif à un caractère d’un groupe constitué de la réunion de deux groupes dont les effectifs et les pourcentages relatifs à ce caractère sont connus. Par exemple l’élève peut calculer le pourcentage d’élèves d’une classe de 30 élèves jouant d’un instrument de musique sachant qu’il y a 15 filles et que 40 % des filles et 20 % des garçons jouent d’un instrument de musique.

Division de deux rationnels

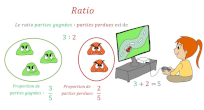
Ratio et fraction d'une quantité

Ratio. Exprimer la proportionnalité entre deux suites de nombres par des égalités de rapports des nombres correspondants.

Volume d'une pyramide - Volume d'un cône de révolution

Volume d'une pyramide et d'un cône de révolution. Conversions.

Comparer deux nombres ou deux grandeurs à l’aide de leur rapport

L’élève comprend que le quotient de deux nombres ou grandeurs permet de les comparer. Il peut s’agir d’une comparaison de deux grandeurs de même nature (rapport de linéarité) ou de deux grandeurs de nature différente en situation de proportionnalité (coefficient de proportionnalité). Pour deux nombres ou grandeurs, on peut employer le terme de « ratio », qui est dans ce cas synonyme de rapport.

Notation scientifique

Raisonnement et démonstration

Implication, contre-exemple, structure de preuve dans des contextes géométriques ou algébriques simples

Statistiques (2) : résolution de problèmes

Résoudre des problèmes faisant intervenir les différents indicateurs. Résoudre des problèmes de comparaison de séries statistiques.

Proportionnalité (3) : ratio et méthode de Singapour

Résoudre des problèmes de partage proportionnel en utilisant le diagramme en barres.

Droite des milieux : connaître et utiliser les théorèmes

Appliquer une augmentation ou une diminution exprimée en pourcentages

Sur des exemples, l’élève remarque qu’augmenter une grandeur de 15 % revient à la multiplier par 1 + 15/100 = 1,15 et que diminuer une grandeur de 20 % revient à la multiplier par 1 - 20% = 0,8. Ce travail préfigure ce qui sera fait en classe de troisième.

Programmes de calcul équivalents ?

Equations ax+b = cx + d - Mise en équation d'un problème

Patron d'une pyramide et d'un cône de révolution

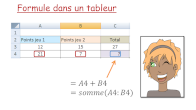
Statistiques (3) : tableur

L’élève utilise le tableur, lorsqu’il doit traiter un grand nombre de valeurs dans une série, pour déterminer les indicateurs de la série. L’élève utilise les fonctions « somme, moyenne, médiane, max, min et nb » du tableur. Interprétation du résultat.

Probabilités (3) : aspect fréquentiel de la probabilité

À partir de la répétition d’une expérience aléatoire, réalisée matériellement ou simulée, comparer des graphiques de distributions (fréquentielle et théorique). Observer la fluctuation des fréquences pour un nombre de répétitions fixé de l'expérience aléatoire.

Notion de fonction - représentation graphique

Produire une formule littérale représentant la dépendance de deux grandeurs. Représenter l’expression d’une grandeur en fonction d’une autre par un graphique. L’élève sait, par exemple, exprimer l’aire restante si on enlève quatre carrés superposables aux quatre coins d'un rectangle de 20 cm de longueur et 13 cm de largeur et construire la représentation graphique de l'aire blanche en fonction de la longueur du côté des carrés. L’élève comprend que la dépendance d’une grandeur en fonction d’une autre peut se traduire par un tableau de valeurs, une formule, ou un graphique.